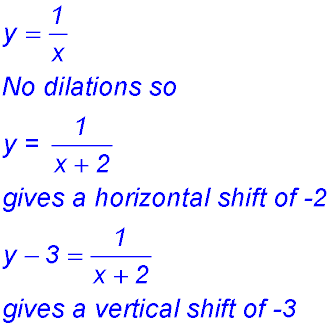Functs - Trans - TYS 1 Solns

Remember when determining SHIFTS, we need to change a given equation into the form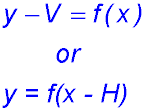

When determining DILATIONS, we need to change a given equation into the form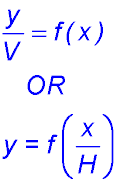

Also remember that it is generally better to do the dilations before doing the shifts.

Shift only	1. When y = x² is shifted 2 units left: y = (x + 2)²	2. When y = x³ is shifted 3 units right: y = (x - 3)³
	3. When y = 5^x is shifted 5 units down: y + 5 = 5^x or y = 5^x - 5	4. When y = x - 5 is shifted 2 units up: y - 2 = x - 5 or y = x - 3
	5. Shifting 3 units to the left changes y = 5x² + 2 to y = 5(x + 3)² + 2	6. Shifting 0.5 units up changes y = 2√x - 2.6 to y - 0.5 = 2√x - 2.6? So y = 2√x - 2.1.
	7. Shifting 6 units down changes y = 5 to y = -1.	8. Shifting 2 units to the right changes x = -4 to x = -2.
Dilation only	9. Dilating y = x²vertically by a factor of 2 gives y/2 = x² or y = 2x².	10. Dilating y = 2^x vertically by a factor of 1/3 gives 3y = 2^x (after dividing y by 1/3).
	11. Dilating 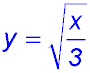horizontally by a factor of 3 gives .	12. Dilating y = x² horizontally by a factor of 0.5 gives
	13. The original parabola has x intercepts at x = -2 and x = 1 and a vertex at (-0.5, -2.25). Dilating y = (x - 1)(x + 2) horizontally by a factor of 3 (i.e. expanding or dilating it horizontally) but no shift requires dividing the x terms in BOTH bracketed terms by 3: So both the vertex and the x intercepts are dilated - i.e. multiplied by 3 - so the x intercepts change to x = -6 and x = 3 (i.e. the original values are multiplied by 3) and the new vertex is at(-1.5, -2.25). These changes are NOT the same as horizontal shifting because then all movements would be by a constant amount.	14. Dilating y = (x - 1)(x + 2) vertically by a factor of 3 gives Hence the x intercepts remain at x = -2 and x = 1. The x value for the vertex remains at x = -0.5 but the y value is tripled from y = -2.25 to y = -6.75. The parabola rises three times as fast as previously.
Identify the shift	15. To track the change of y = 2x² + 1 to y = 2x² - 3 we rewrite to isolate the original equation: y = (2x² + 1) - 4. ∴ y + 4 = (2x² + 1) So there is a vertical shift of -4. All y values are reduced by 4.	16. To track the change of y = 4x³ to y = 4 (x + 2)³, no rewriting is necessary as it is in the relevant format. There is a horizontal shift of -2. For example the x intercept changes from x = 0 to x = -2.
	17. To change y = x² + y² to y = (x + 1)² + (y - 2)² there is a horizontal shift of -1 and a vertical shift of 2.	18. To change y = sin x to y = sin (x - π) requires a horizontal shift of π units to the right.
Identify the dilation	19. To transform y = 2x² to y = 4x², rewrite as y = 4x² = 2(2x²). Hence the effect is a vertical dilation of 2 which stretches all y values by a factor of 2 (i.e. multiplies all y values by 2).	20. To transform y = 3 cos x to y = cos x: The effect of this transformation is to reduce all y values by one third. So the x intercepts remain the same but the maximum values reduce from 3 to 1.
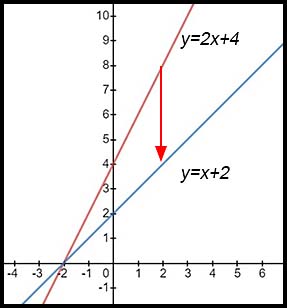
	21. To transform y = 2^x to y = 2^x+2: The effect of the vertical dilation is to change all y values by a dilation factor of 4 (i.e. to multiply all y values by 4 - see especially x = 0).	22. To transform y = 2x + 4 to y = x + 2: The effect of the vertical dilation is to halve all y values for each x value. Hence the point (2, 8) on y = 2x + 4 becomes (2, 4) on y = x + 2.
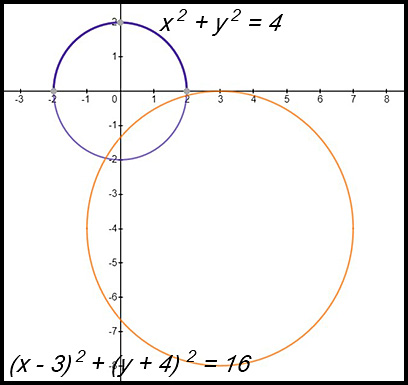
Shift and dilation	23. To change x² + y² = 4 into (x - 3)² + (y + 4)²= 16: horizontal shift of 3; vertical shift of -4; horizontal and vertical dilations of 2. The centre of the original circle is (0, 0). The centre of the transformed circle is (3, -4). The dilation transformations change the radius from 2 to 4. The shift transformations move the centre from x = 0 to x = 3 and from y = 0 to y = -4.	24. The transformation(s) to change x² + y² = 1 into 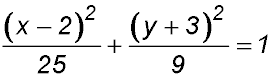require rewriting the equation as: horizontal shift of 2; vertical shift of -3; horizontal dilation (enlargement) of 5; vertical dilation of 3. The circle turns into a horizontal ellipse.
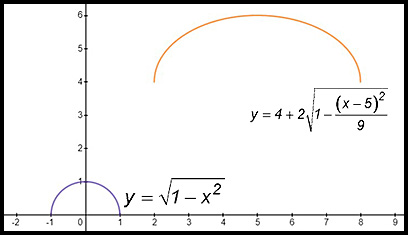
	25. To transform y = cos x into y = 5cos(2x - π/3): So the transformations are: horizontal shift of π/6; no vertical shift; horizontal dilation factor of 0.5; vertical dilation factor of 5.	26. To transform the equation 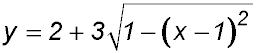to : Start with the vertical dilation: So the transformations are: horizontal shift of 1; vertical shift of 2; no horizontal dilation; vertical dilation with a factor of 3. 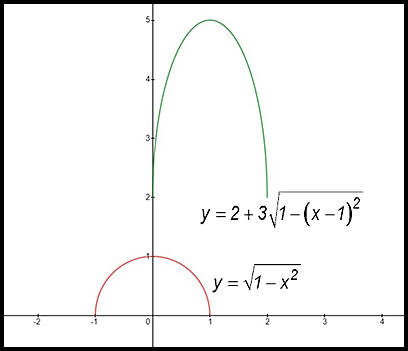The peak of the semi-circle is at (0, 1): the vertical dilation takes (0, 1) to (0, 3); the vertical shift takes (0, 3) to (0, 5); the horizontal shift takes (0, 5) to (1, 5).
	27. To transform the equation to become : It is possible to start transforming the original equation by incorporating the vertical shift: Hence: the horizontal shift is 5; the vertical shift is 4; the horizontal dilation is 3; the vertical dilation is 2. Note in the above graph: the origin (0, 0) moves horizontally 5 units and vertically 4 to (5, 4); the original point (-1, 0) was 1 unit to the left of (0, 0) and the horizontal dilation of 3 results in that distance being extended to -3 units from (5, 4) - so to (2, 4). the original point (0, 1) was 1 unit above (0, 0) and the vertical dilation of 2 results in that distance being extended up 2 units from (5, 4) - so to (5, 6).	28. Starting with the equation what transformations change the equation to ? Transformations are: horizontal shift of -2; vertical shift of -3; no dilations.
	Use the following diagram of y = f(x) = x² to sketch new graphs in response to the information given in each of questions 29-30.
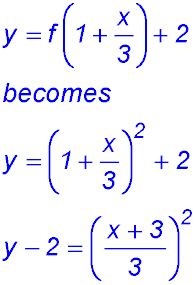
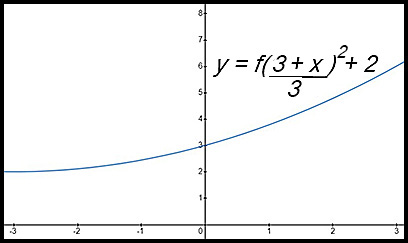
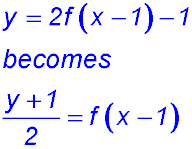
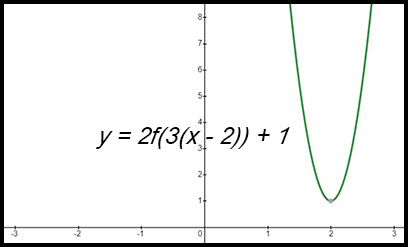
	29. Note: There is a horizontal shift of 3 to the left and a horizontal dilution (expansion) by a factor of 3 (so the curve flattens out). Hence the parabola flattens and the vertex moves to x = -3. There is a vertical shift of 2. Hence the vertex is now at (-3, 2) rather than (0, 0). At x = 0, y = 1 + 2 = 3.	30. Note: there is a horizontal shift of 2 to the right (so the vertex is now at x = 2) and a horizontal dilution of 1/3 (hence the curve becomes narrower). There is a vertical shift of 1 upwards (so the vertex moves to y = 1) and a vertical dilution by a factor of 2 (hence the curve climbs more quickly).
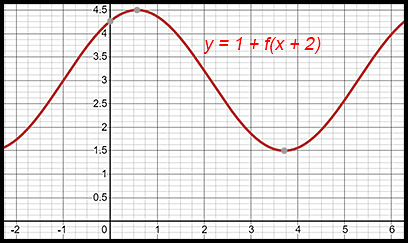
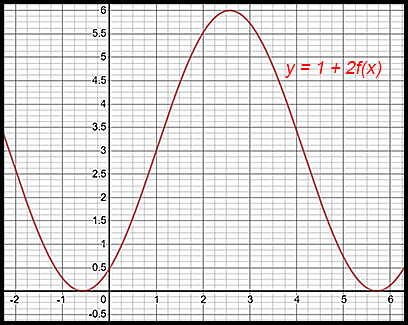
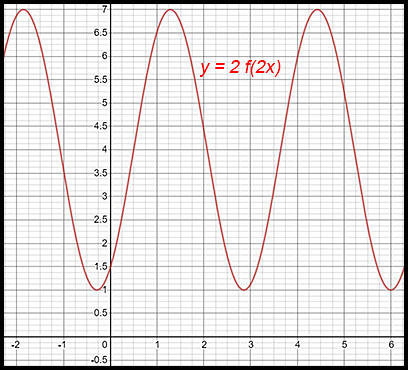
	Use the following diagram of y = f(x) to sketch new graphs in response to the information given in each of questions 31-34.
Diagrams	31. 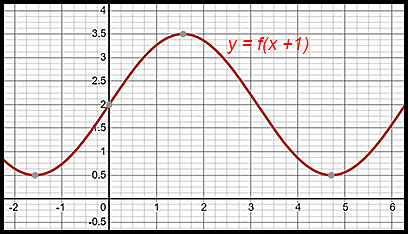Note: The horizontal shift of -1 moves the previous point at x = 1 to the left and it is now on the y axis. The minimum points at about x = -0.5 and x = 5.75 have moved left to about x = -1.5 and to about x = 4.75 . There is no vertical change.	32. Note: The previous centre of the loops was at y = 2. The vertical shift of 1 has shifted the central y value up to y = 3. The previous range was from 0.5 to 3.5 and that has changed to a range from 1.5 to 4.5. The horizontal shift of -2 moves the maximum point from about x = 2.5 to the left to x = 0.5. The next minimum at about 3.5 has therefore been shifted left to about 1.5.
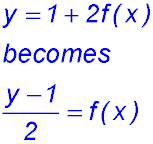
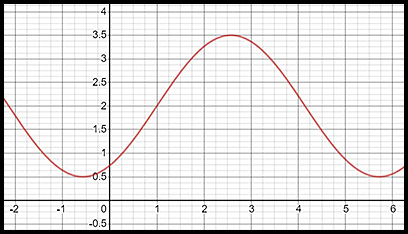
	33. Note: The previous centre of the loops was at about y = 2 with a minimum of y = 0,5 and a maximum of y = 3.5 (a difference of 3). The vertical shift of 1 moves the centre between the peaks and troughs from y = 2 to y = 3. The vertical dilation of 2 changes one minimum value to y = 0 at x = -0.5 and one maximum value to y = 6 at x = 2.5 respectively (a difference of 6 which is twice the original amplitude). There is no horizontal shift or dilation.	34. 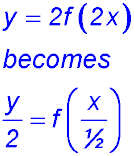Note: There is a horizontal dilation of ½ which compresses the pattern. Previously one of the lowest points occurred at x = ½ whereas now, the corresponding lowest point is at x = ¼. The distances between the two troughs was originally 6 units but is now 3 units. The distance above the y axis was originally ½ but it is now 1. The vertical dilation of a factor of 2 increases the amplitude of thepattern from 3 units to 6 units.
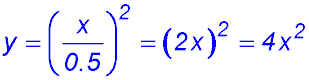
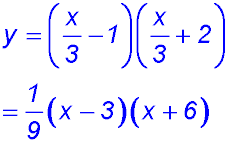
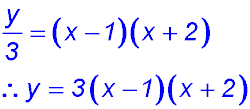
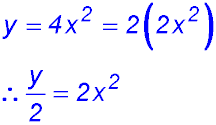
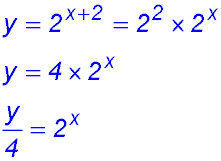
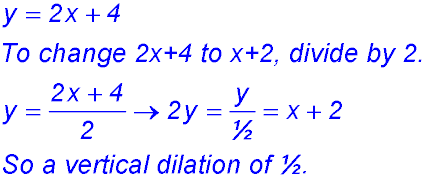
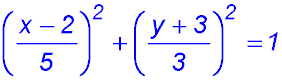
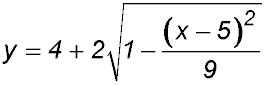
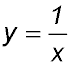
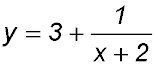